RE-WISE method principle
Warning : This text contains mathematic formulas, considered by some readers harmful to their health.
Encouragement : The worst functions we can ever see in the text are logarithms and exponentials. So even a high school student can confidently continue to read.
Learning and forgetting
The majority of us know from their own experience that we will soon forget what we just learned. It is very difficult to remember a phone number of your own new cell phone, and to go grocery shopping without a list is almost dangerous. We forget the names of people who introduce themselves to us often several seconds later.
But at the end, we will surprisingly keep something in our head. We remember hundreds of names, thousands of words from a foreign language, even the phone number of our first love we dated thirty years ago. How come?
Folk wisdom says that “Repetition is the mother of wisdom”. There is something to it, but one can not rely on it completely. Dishing up the material the evening before the test again and again does not work very well. On the other hand, there are things which we remember almost incidentally that we almost do not notice.
It seems that not only the repetitions themselves are important, but also the intervals between them. It seems that there is a certain suitable rhythm of review, an optimum mode in which we learn the most and struggle the least.
This text describes how the RE-WISE method approaches the problem. RE-WISE is a tutorial method by LANGMaster for learning vocabulary in foreign languages. It is also suitable for repetition of simple facts from other fields.
Forgetting curve
The experiment shows that our ability to maintain new information in our memory drops very quickly – in a geometrical progression. On the second day, we will remember roughly half of what we have learned yesterday. On the third day, only a half of that half and so on.
Written in a formula, we remember from the learnt:
1/2m
- m is the number of days passed from learning.
Such a forgetting curve is very saddening for any student.
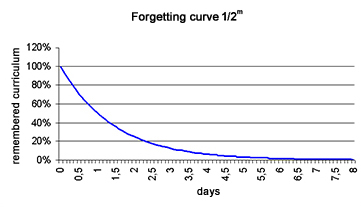
Repetition curve
On the other hand, the dangerous exponential function plays a positive role in another observation. Let’s remember the material well, review it the next day, then in the next two, four, eight days…
Expressed in mathematics: the number of days for which we remember the material grows pursuant to the formula:
2n
- n is the number of repetitions of the fact.
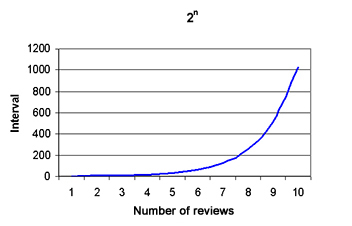
If it is true, it is very good news.
Let’s elaborate the sequence a bit further:
|
Review no.:
|
Interval before next repetition
|
|
0
|
1 day |
|
1
|
2 days |
|
2
|
4 days |
|
3
|
8 days |
|
4
|
16 days |
|
5
|
1 month, 2 days |
|
6
|
2 month, 4 days |
|
7
|
4 months, 8 days |
|
8
|
8 months, 16 days |
|
9
|
1 year, 4 months, 27 days
|
|
10
|
2 years, 9 months, 24 days |
|
11
|
5 years, 7 months, 13 days
|
|
12
|
11 years, 2 months, 21 days |
|
13
|
22 years, 5 months, 12 days |
|
14
|
44 years, 10 months, 24 days |
As a whole, we have a schedule in front of us for almost 90 years. In other words, with thorough planning, we can only need fourteen repetitions after the first learning to remember the fact for our entire life. Several individuals from some Georgian Mountains might maybe need a fifteenth repetition, but that’s really the maximum.
There is one more promising consideration: Let’s imagine that we are willing to learn 10 new words daily, and repeat 100 old ones at most. This still looks bearable. If we proceed according to the outlined plan, we will pass these limits at the earliest when we arrive at the eleventh repetition of the very first ten words. Thus in 5 years, 7 months and 13 days. By then we will already know more than 20 thousands words, which corresponds to the solid vocabulary of an adult.
Plan for improving the mathematical model
It could seem we reached the goal. Let’s write software which will submit the words and phrases for repetition after 1, 2, 4, 8, etc. days and we are done.
Many rightful objections can be raised against such a simple model:
- Each word is different. Some are easy to learn, some are not.
- Every person is different. One has a bad memory and needs to repeat more often. Other remembers well and could have longer intervals.
- We have already seen some of the expressions we are entering in the software. Maybe we should not start with a repetition interval of 1 day, but maybe of 4 or 8.
- We will go for vacations, or maybe we just temporarily get overwhelmed by laziness and we will not study for a while. We will miss the recommended moment for repetition and we will return to studying later than the program recommended. Shall we shorten up the repetition interval? By how much?
We want to create a more perfect model, which will address these objections, but “in the average” will behave similarly optimistically as the basic idea with repetition in the interval n.
We will approach this according to this plan:
- We will propose a formula which will discover how much we remember the material.
- The formula will also model the fact that repetition extends the interval for which we still remember the material.
- We will write down the evaluation the student gets during the individual repetitions. We will monitor how much his/her memory deviates from our forecast.
- We will preserve in the formulas some parameters which will get adapted so the forecast deviation will be as small as possible. That will improve the forecast for future repetitions.
Whoever is not willing to go through all the preliminary considerations and would rather see the result, can peek in the paragraph Summary.
If you want to read everything, continue with the paragraph Basic Terms.