Growth of Stability during repetition
The RE-WISE method therefore recommends to the user to repeat the Fact when he/she partially forgets it, by approx. 30%.
We presume that after repetition, we will remember the Fact for a longer time period, on average twice as long. In the previous proposed formula, we tried to interpret the Stability as the number of days before the next recommended review.
Therefore, it does not surprise us that we suggest the Stability during repetition in the optimum moment increased twice:
STABn+1 = 2*STABn
- STABn is the Stability in n-th repetition.
Let’s stress again that the formula applies only provided the student reviews at the optimal moment.
In such a case, how will the optimum course of the Retrievability look? After each repetition, it will jump to 100% and then it will gradually decrease. But the decrease will be slower after each review.
Example:
We will use the proposed formulas for RET and STAB.
Let’s choose OFI = 30%. Then, we will repeat when RET drops under 70%.
The forgetting curve will then look like this:
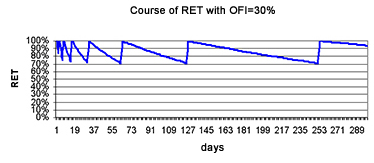
Note: The decreasing parts of the curve are not straight lines, but in the introductory part are well straightened reversed exponentials – curves 1/2(m*SN/STAB.
The basis of the geometric sequence (Base Factor)
Why should the Stability increase exactly 2x in the moment of optimum repetition? Why not 2.2 x or 1.5 x? Each word has a different difficulty and each person has a different memory. Let’s replace the number two in the formula with a calculation of the Stability with a parameter and let’s call it the Base Factor. At the beginning of learning, we will presume its value is 2 and we will try to determine its value from the course of repetition. But more about this in a minute.
So far, we have arrived at the opinion that the stability will grow according to the formula:
STABn = (Base Factor)n
- n is the number of repetitions.
- Base Factoris a number based on the Fact’s difficulty and the student’s memory and its value is usually somewhere around 2.
Initial Stability (iniStab)
For the initial zero repetition, the Stability is:
(Base Factor)n = 1
We can ask again, why the initial value of the Stability should equal 1.
Let’s imagine that we have been learning for a while using the RE-WISE method, and achieved the Fact’s stability to equal 20. However, the Base Factor (the base of the geometric sequence of the growing Stability) is still 2, because the Fact is still – average – difficult.
But – oh my God – the disk collapses and we lose our data. We would be brave to start learning from scratch. We review in one, two, four days and we respond correctly, we don’t forget. If the algorithm only adjusts the Base Factor value, it would assume that the Fact is too easy for you and would initiate to increase the Base factor. But that’s not correct. The Fact is still the same difficulty, but we already knew it a bit at the beginning. The algorithm should guess after a while that the correct value of the Base Factor is still 2, but that it should have actually started from the Stability value 20.
We will implement one more parameter for he difficulty of a Fact. We will call it the Initial Stability (iniStab) and will assume at the beginning that it equals 1.
Therefore, we improved the formula for calculation of the Stability:
STABn = iniStab * (Base Factor)n
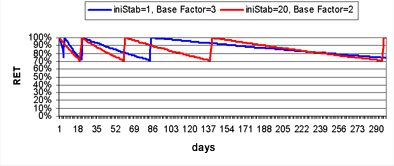
The chart compares the course of the repetition curve for the increased Base Factor parameter against the increase of iniStab. The curve with the higher Base Factor will always eventually run out the curve with the higher iniStab value. This should be supported by the predicament, that by the adjustment of one parameter, we can not compensate the change of the second one and that therefore, we should try to search for a suitable combination of both.
Change of Stability (CHNG)
As we stressed several times, the suggested formula is valid only when it repeats in optimal moment. We assume that this moment will occur when we forget the Fact by 30%.
But what will happen if we repeat the Fact at other times than at this optimum moment? The Stability will increase differently every time, depending on the immediate value of the Retrievability.
Let’s generalize the formula for stability growth as follows:
STABn+1= CHNG(RETn, Base Factor)*STABn
for n >= 0
STAB0 = iniStab
- CHNG(RETn, Base Factor) is a function depending on the Retrievability value at the moment of repetition. It maximally reaches the Base Factor value.
- RETn is the real Retrievability value estimated using the point evaluation in the appropriate repetition. Points can be awarded by the software provided it is able to automatically evaluate the answer, or we can ask the student to evaluate himself concerning the extent to which he/she remembered the fact.
- IniStab and Base Factor are numbers, which characterize the difficulty of a Fact. At the beginning, we assume that they have values IniStab=1 and Base Factor=2. However, we will try to adapt them according to the course of repetition. The adaptation details will be revealed later; first we must define more precisely the CHNG function.
The form of the CHNG function
How should the function look which will tell us, based on the Retrievability, how many times the Stability increases?
We have three hypotheses for the proposal of its basic shape:
- The first hypothesis on Stability change says: “If I keep reviewing the Fact quickly and repeatedly (with high Retrievability), the Stability does not grow much”. In other words, if Retrievability is close to 100%, the CHNG change will near to 1:
limRET->100%CHNG(RET) = 1
- The second hypothesis on Stability change says: “If I review the fact with a suitable time delay, the Stability increases”. With a bit of fantasy, this can be interpreted as indicating that there is an optimum level Optimal Forgetting Index (OFI) at which the CHNG maximizes. This maximum should be equal to the Base Factor (approximately 2):
Base Factor = CHNG(100%-OFI) >= CHNG(RET)0 <= RET <= 100%
- The third hypothesis says: “After forgetting the Fact (Retrievability drops under a certain level), the Stability disappears quickly.” Therefore, if Retrievability is approaching 0%, the change of Stability is also approaching 0.
limRET->0CHNG(RET) = 0
Between these points, we recommend stringing a suitable curve, which would be continuous and neatly curved. These requirements could be met for example by a function composed of two parabolas. They both have their peak in 1-OFI, one of them goes through the point (0,0), and the second goes through the point (1,1).
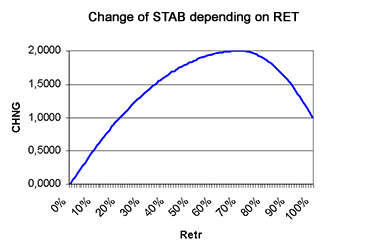
A critical reader can object at this moment that we came up with the curve based on values of a function at three points. The possible response is, for example, that we will never learn the value of the Retrievability from the student with accuracy within one percent. In the RE-WISE method, the user evaluates him/her self on a scale from 0-4 points, therefore very roughly. Therefore, the precise shape of the curve does not matter that much.
Deducting a formula for these parabolas requires a high school struggle and we don’t dare to bother the reader with it.
We will limit ourselves to the statement that the formula for the parabola is:
y = Ax2 + Bx + C
We have two parabolas, instead of x we write RET and instead of y we write CHNG:
CHNG = A1*RET2 + B1*RET + C1
for RET >= 1 - OFI
CHNG = A2*RET2 + B2*RET + C2
for RET <= 1 - OFI
Furthermore, we know the value of each parabola at two points – on the edge and at the peak.
- For RET = 0, the result should be 0.
- For RET = 1, the result should be 1.
- For RET = 1 - OFI the result should be maximum – Base Factor.
Besides, we know that in point 1 – OFI, both functions have their maximum, therefore their first derivation equals zero.
That’s a lot of equations to arrive with a certain effort to the values of the coefficients:
A1 = (1 - Base Factor) / OFI2
B1 = -2 * (1 - OFI) * A1
C1 = 1 - (1 - 2 * (1 - OFI)) * A1
A2 = -Base Factor / (1 - OFI)2
B2 = -2 * (1 - OFI) * A2
C2 = 0
So, we suggested a formula, which models forgetting the learned Facts. The formula will even be able to predict what evaluation the student will get at next repetition. But what will we do, if the student gets more points, or less? We would like to somehow adjust our formula to the real results and make the next forecasts more precise. This is covered in the paragraph Adaptation according to grades.